동시발생 행렬
[자연어 처리/NLP기초] 5. 통계 기반 기법: 동시발생 행렬
단어의 분산 표현과 분포 가설 https://seokii.tistory.com/93 [자연어 처리/NLP기초] 4. 단어의 분산 표현과 분포 가설 말뭉치와 말뭉치 전처리하기 https://seokii.tistory.com/91 [자연어 처리/NLP기초] 3. 말..
seokii.tistory.com
지난 글에서 동시발생 행렬을 공부하고 해당 내용을 정리했었습니다.
코사인 유사도
벡터 사이의 유사도를 측정하는 방법은 여러 가지가 있는데, 코사인 유사도를 사용해서 단어 벡터의 유사도를 구해보도록 하겠습니다.
코사인 유사도는 두 벡터 \( x = (x_{1}, x_{2}, x_{3}, ... , x_{n} )\)과 \( y = (y_{1}, y_{2}, y_{3}, ... , y_{n} )\)가 존재한다면 다음 식으로 정의할 수 있습니다.
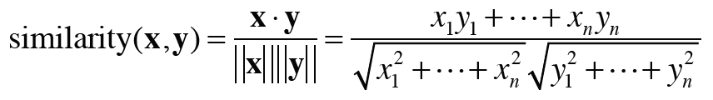
분자에는 백터의 내적을, 분모에는 각 벡터의 노름(놈, norm)이 나옵니다.
노름(norm)은 벡터의 크기를 나타낸 것이며 위의 식에서는 'L2 노름'을 계산합니다.
(L2 노름은 벡터의 각 원소를 제곱해 더한 후 다시 제곱근을 구해 계산함.)
식의 핵심은 벡터를 정규화하고 내적을 구하는 것입니다.
코사인 유사도는 다음과 같이 구현할 수 있습니다.
import numpy as np
def cos_similarity(x, y, eps=1e-8):
nx = x / np.sqrt(np.sum(x**2) + eps)
ny = y / np.sqrt(np.sum(y**2) + eps)
return np.dot(nx, ny)여가서 eps는 0으로 나눌때 오류가 발생하므로, 분모에 아주 작은 값을 더해준 것입니다.
지금까지 정리했었던 내용과 코드들을 바탕으로 코사인 유사도를 계산해보는 코드입니다.
import numpy as np
def preprocess(text):
text = text.lower()
text = text.replace('.', ' .')
words = text.split(' ')
word_to_id = {}
id_to_word = {}
for word in words:
if word not in word_to_id:
new_id = len(word_to_id)
word_to_id[word] = new_id
id_to_word[new_id] = word
corpus = np.array([word_to_id[w] for w in words])
return corpus, word_to_id, id_to_word
def create_co_matrix(corpus, vocab_size, window_size=1):
corpus_size = len(corpus)
co_matrix = np.zeros((vocab_size, vocab_size), dtype=np.int32)
for idx, word_id in enumerate(corpus):
for i in range(1, window_size + 1):
left_idx = idx - i
right_idx = idx + i
if left_idx >= 0:
left_word_id = corpus[left_idx]
co_matrix[word_id, left_word_id] += 1
if right_idx < corpus_size:
right_word_id = corpus[right_idx]
co_matrix[word_id, right_word_id] += 1
return co_matrix
def cos_similarity(x, y, eps=1e-8):
nx = x / np.sqrt(np.sum(x**2) + eps)
ny = y / np.sqrt(np.sum(y**2) + eps)
return np.dot(nx, ny)
text = 'You say goodbye and I say hello.'
corpus, word_to_id, id_to_word = preprocess(text)
vocab_size = len(word_to_id)
C = create_co_matrix(corpus, vocab_size)
c0 = C[word_to_id['you']] # "you"의 단어 벡터
c1 = C[word_to_id['i']] # "i"의 단어 벡터
print(cos_similarity(c0, c1))0.7071067758832467"you"라는 단어와 "i"라는 단어의 코사인 유사도는 0.7071... 으로 나왔습니다. 코사인 유사도의 값은 -1 ~ 1의 값이므로 유사성이 크다고 볼 수 있습니다.
'머신러닝 & 딥러닝 > 자연어처리' 카테고리의 다른 글
| [NLP] 네이버 영화 리뷰 데이터(nsmc) 감성 분석 - CNN (0) | 2022.06.30 |
|---|---|
| [NLP] 네이버 영화 리뷰 데이터(nsmc) 감성 분석 - LSTM (2) | 2022.06.21 |
| [자연어 처리/NLP기초] 5. 통계 기반 기법: 동시발생 행렬 (0) | 2022.02.21 |
| [자연어 처리/NLP기초] 4. 단어의 분산 표현과 분포 가설 (2) | 2022.02.21 |
| [자연어 처리/NLP기초] 3. 말뭉치와 말뭉치 전처리하기 (0) | 2022.02.19 |




댓글